CS1 Consumption/saving model with borrowing constraint
This is an implementation of the model in Deaton (1991).
Contents
Model's structure
Response variable Consumption (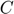 ).
).
State variable Cash on hand (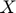 ).
).
Shock Labor income (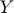 ).
).
Parameters Interest rate ( ), Rate of time preference (
), Rate of time preference (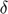 ), and Elasticity of intertemporal substitution (
), and Elasticity of intertemporal substitution (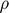 ).
).
Equilibrium equation
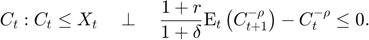
Transition equation
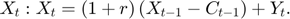
Writing the model
The model is defined in a Yaml file: cs1.yaml.
Create the model object
Mean and standard deviation of the shocks
Mu = 100; sigma = 10;
You generate the MATLAB model file and pack the model object with the following command
model = recsmodel('cs1.yaml',... struct('Mu',Mu,'Sigma',sigma^2,'order',5));
Deterministic steady state (equal to first guess)
State variables:
X
___
100
Response variables:
C
___
100
Expectations variables:
E
______
0.0001
This command creates a MATLAB file, cs1model.m, containing the definition the model and all its Jacobians from the human readable file cs1.yaml.
Define approximation space
[interp,s] = recsinterpinit(20,model.sss/2,model.sss*2);
First-guess: Consumption equal to cash on hand
x = s;
To force the solver to compute the approximation of the expectations function, it is necessary to add at least an empty value for interp.ch
interp.ch = [];
Solve for rational expectations
[interp,x] = recsSolveREE(interp,model,s,x);
Successive approximation
Major Minor Lipschitz Residual
0 0 1.08E+02 (Input point)
1 1 0.6916 3.35E+01
2 1 0.5517 1.50E+01
3 1 0.4800 7.82E+00
4 1 0.4413 4.37E+00
5 1 0.4210 2.53E+00
6 1 0.4128 1.49E+00
7 1 0.4128 8.74E-01
8 1 0.4145 5.12E-01
9 1 0.4179 2.98E-01
10 1 0.4232 1.72E-01
11 1 1.0000 0.00E+00
Solution found - Residual lower than absolute tolerance
Plot the decision rule
figure plot(s,[x s]) legend('Policy rule','45 degree line') legend('Location','NorthWest') legend('boxoff') xlabel('Cash on hand') ylabel('Consumption')
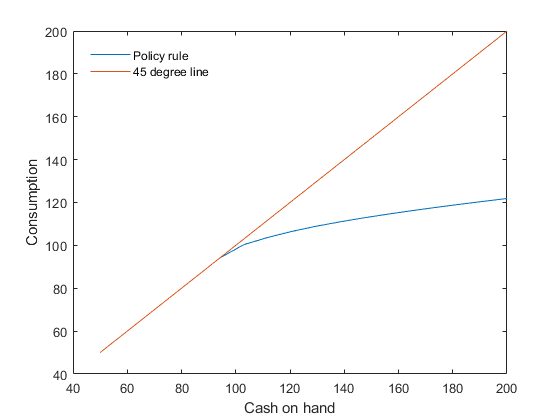
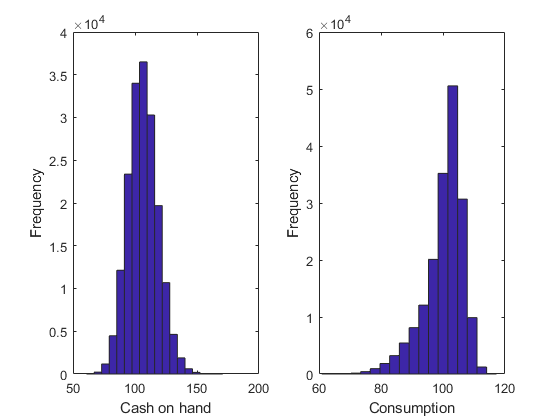
Simulate the model
[~,~,~,stat] = recsSimul(model,interp,model.sss(ones(1000,1),:),200); subplot(1,2,1) xlabel('Cash on hand') ylabel('Frequency') subplot(1,2,2) xlabel('Consumption') ylabel('Frequency')
Statistics from simulated variables (excluding the first 20 observations):
Moments
Mean StdDev Skewness Kurtosis Min Max pLB pUB
______ ______ ________ ________ ______ ______ ___ ______
X 106.46 11.993 0.21404 3.1685 60.906 170.81 NaN NaN
C 100.3 6.3358 -1.2064 4.8722 60.904 117.21 0 12.001
Correlation
X C
_______ _______
X 1 0.94694
C 0.94694 1
Autocorrelation
T1 T2 T3 T4 T5
_______ _______ _______ ________ ________
X 0.50523 0.26951 0.14663 0.073857 0.035042
C 0.38738 0.19105 0.10297 0.049875 0.022239
References
Deaton, A. (1991). Saving and liquidity constraints. Econometrica, 59(5), 1221-1248.