Solution methods
This page describes the default algorithm used in RECS to solve for a model's rational expectations equilibrium. It is possible to choose other methods by changing the options.
The numerical algorithm used here is inspired by Fackler (2005) and Miranda and Fackler (1995). It is a projection method with a collocation approach solved by time iteration and approximation of the behavior of response variables.
Contents
Default algorithm
The method will attempt to find a function that approximates well the behavior of response variables,
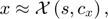
where 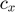 are the parameters defining the approximation. To calculate this approximation, we discretize the state space, and the spline has to hold exactly for all points of the grid. By default, RECS uses a spline approximation of response variables as a function of state variables,
are the parameters defining the approximation. To calculate this approximation, we discretize the state space, and the spline has to hold exactly for all points of the grid. By default, RECS uses a spline approximation of response variables as a function of state variables,
The expectations operator is replaced by a sum over possible realization of shocks, 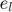 , to which are associated the probability
, to which are associated the probability 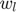 . If shocks are normal, the pairs
. If shocks are normal, the pairs 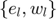 are calculated by RECS using a Gaussian quadrature. Using this discretization, we can express the equilibrium equation as
are calculated by RECS using a Gaussian quadrature. Using this discretization, we can express the equilibrium equation as
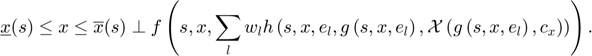
For a given approximation, 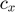 , and a given
, and a given  , this equation is a function of
, this equation is a function of 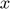 only and can be solved using a mixed complementarity solver.
only and can be solved using a mixed complementarity solver.
Once all the above elements are defined, we can proceed to the algorithm, which runs as follows:
- Initialize the approximation,
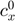 , based on a first guess,
, based on a first guess, 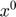 .
. - For each point of the grid of state variables,
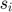 , solve for
, solve for 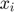 using an MCP solver the following equation:
using an MCP solver the following equation: 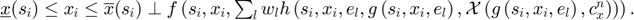
- Update the approximation using the new values of response variables,
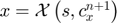 .
. - If
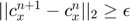 then increment
then increment 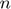 to
to 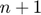 and go to step 2.
and go to step 2.
References
Miranda, M. J. and Fackler, P. L. (2002). Applied Computational Economics and Finance. Cambridge: MIT Press.