STO5 Two-country storage-trade model
Model close to Miranda and Glauber (1995). Countries  and
and 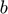 are indicated by the subscript
are indicated by the subscript 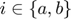 . When variables corresponding to both countries appear in the same equation, the foreign country is indicated by the subscript
. When variables corresponding to both countries appear in the same equation, the foreign country is indicated by the subscript 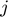 .
.
Contents
Model's structure
Response variables Storage (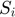 ), Planned production (
), Planned production (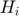 ), Price (
), Price (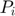 ) and Export (
) and Export (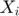 ).
).
State variable Availability (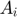 ).
).
Shock Productivity shocks (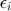 ).
).
Parameters Unit physical storage cost (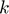 ), Depreciation share (
), Depreciation share (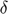 ), Interest rate (
), Interest rate ( ), Scale parameter for the production cost function (
), Scale parameter for the production cost function (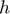 ), Inverse of supply elasticity (
), Inverse of supply elasticity (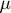 ), Demand price elasticity (
), Demand price elasticity (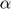 ), Scale parameter for demand function (
), Scale parameter for demand function (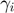 ), Trade cost (
), Trade cost (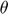 ) and Tariff (
) and Tariff (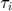 ).
).
Equilibrium equations
For 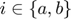 and
and 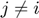 :
:
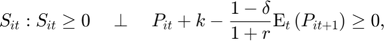
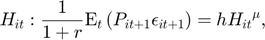
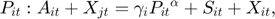

Transition equation
For 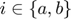 :
:
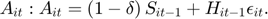
Writing the model
The model is defined in a Yaml file: sto5.yaml.
Create the model object
Mu = [1 1];
sigma = [0.05 0;
0 0.05];
model = recsmodel('sto5.yaml',struct('Mu',Mu,'Sigma',sigma^2,'order',7));
Deterministic steady state (different from first guess, max(|delta|)=0.31777)
State variables:
Aa Ab
______ ______
1.0402 1.0567
Response variables:
Sa Sb Ha Hb Pa Pb Xa Xb
__ __________ ______ ______ ______ ______ ________ __
0 8.4168e-19 1.0402 1.0567 1.2178 1.3178 0.078829 0
Expectations variables:
EPa EPb EPea EPeb
______ ______ ______ ______
1.2178 1.3178 1.2178 1.3178
Define approximation space
[interp,s] = recsinterpinit(15,0.73*model.sss,2*model.sss);
Find a first guess through the perfect foresight solution
interp = recsFirstGuess(interp,model,s,model.sss,model.xss,struct('T',5));
Solve for rational expectations
[interp,x] = recsSolveREE(interp,model,s);
Successive approximation
Major Minor Lipschitz Residual
0 0 7.73E-01 (Input point)
1 1 0.8943 2.14E-01
2 1 0.9616 9.75E-02
3 1 0.7867 7.31E-02
4 1 0.6319 4.34E-02
5 1 0.6484 1.69E-02
6 1 0.7361 4.49E-03
7 1 0.7768 1.00E-03
8 1 0.7905 2.10E-04
9 1 0.7945 4.32E-05
10 1 0.7958 8.82E-06
11 1 0.7962 1.80E-06
12 1 0.8031 3.74E-07
13 1 0.9038 8.46E-08
14 1 1.0000 0.00E+00
Solution found - Residual lower than absolute tolerance
Simulate the model
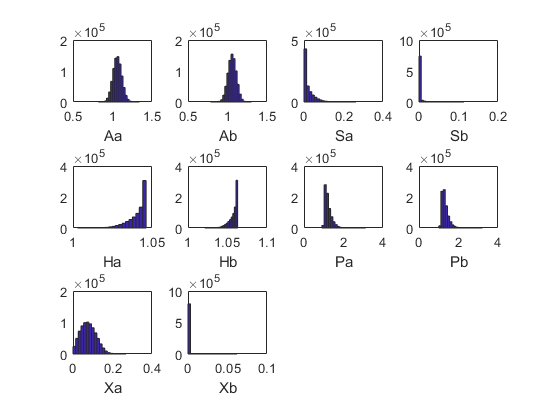
[~,~,~,stat] = recsSimul(model,interp,model.sss(ones(1E4,1),:),100);
Statistics from simulated variables (excluding the first 20 observations):
Moments
Mean StdDev Skewness Kurtosis Min Max pLB pUB
__________ __________ _________ ________ _______ ________ _______ ___
Aa 1.0615 0.056021 0.079139 3.0594 0.82001 1.342 NaN NaN
Ab 1.0588 0.053172 0.0023208 3 0.78352 1.3038 NaN NaN
Sa 0.021354 0.02686 1.7747 6.5435 0 0.26334 20.218 0
Sb 0.0014208 0.0049854 6.2295 57.578 0 0.11381 70.087 0
Ha 1.0406 0.005748 -1.4948 5.0673 1.0027 1.0463 0 0
Hb 1.0574 0.0054542 -1.5047 5.0917 1.0214 1.0628 0 0
Pa 1.2222 0.17537 1.5246 6.0402 0.90647 3.1226 0 0
Pb 1.3242 0.17191 1.5469 6.4956 0.99882 3.2159 0 0
Xa 0.077861 0.038788 0.33209 2.6835 0 0.26816 0.15363 0
Xb 0.00016171 0.00086318 23.532 798.22 0 0.061958 44.815 0
Correlation
Aa Ab Sa Sb Ha Hb Pa Pb Xa Xb
_________ _________ _________ _________ ________ ________ ________ ________ ________ _________
Aa 1 -0.032507 0.68347 -0.084515 -0.64564 -0.64578 -0.66163 -0.66965 0.52251 -0.20812
Ab -0.032507 1 0.53128 0.52702 -0.605 -0.60358 -0.63603 -0.63559 -0.84956 0.1135
Sa 0.68347 0.53128 1 0.1961 -0.98168 -0.98219 -0.65901 -0.67349 -0.182 -0.060681
Sb -0.084515 0.52702 0.1961 1 -0.36548 -0.36373 -0.21845 -0.22125 -0.4213 0.07748
Ha -0.64564 -0.605 -0.98168 -0.36548 1 0.99999 0.68427 0.6972 0.24316 0.055652
Hb -0.64578 -0.60358 -0.98219 -0.36373 0.99999 1 0.68284 0.69585 0.24239 0.05576
Pa -0.66163 -0.63603 -0.65901 -0.21845 0.68427 0.68284 1 0.99549 0.15623 0.10826
Pb -0.66965 -0.63559 -0.67349 -0.22125 0.6972 0.69585 0.99549 1 0.15001 0.047489
Xa 0.52251 -0.84956 -0.182 -0.4213 0.24316 0.24239 0.15623 0.15001 1 -0.16019
Xb -0.20812 0.1135 -0.060681 0.07748 0.055652 0.05576 0.10826 0.047489 -0.16019 1
Autocorrelation
T1 T2 T3 T4 T5
__________ _________ _________ _________ _________
Aa 0.22939 0.02947 -0.010715 -0.01749 -0.020583
Ab -0.028468 -0.024722 -0.01517 -0.012473 -0.012601
Sa 0.1978 0.022797 -0.011241 -0.017322 -0.018987
Sb 0.0060039 -0.016106 -0.014682 -0.013809 -0.01206
Ha 0.18214 0.019869 -0.011336 -0.017478 -0.018262
Hb 0.18243 0.01992 -0.011329 -0.017489 -0.018273
Pa 0.10913 0.0078086 -0.013164 -0.016746 -0.016546
Pb 0.11533 0.0090659 -0.013051 -0.016779 -0.016571
Xa -0.030315 -0.026361 -0.015005 -0.011474 -0.013226
Xb -0.0053893 -0.011814 -0.013243 -0.01292 -0.013993
References
Miranda, M. J. and Glauber, J. W. (1995). Solving stochastic models of competitive storage and trade by Chebychev collocation methods. Agricultural and Resource Economics Review, 24(1), 70-77.