STO6 Quarterly storage model with annual inelastic supply
This model represents the market of a storable commodity that is produced once a year and stored for a year-long consumption. Supply is stochastic and inelastic. Except for its distribution, no information about the coming harvest is known.
Contents
Model's structure
Writing the model
The model is defined in a Yaml file: sto6.yaml.
Create the model object
model = recsmodel('sto6.yaml',struct('Mu',0,'Sigma',0.05^2,'order',5));
Deterministic steady state (different from first guess, max(|delta|)=0.0961408)
State variables:
A1
__
4
Response variables:
S1 S2 S3 S4 P1 P2 P3 P4 A2 A3 A4
______ ______ _______ __________ _______ ______ ______ ______ ______ ______ _______
2.9964 1.9854 0.98671 1.9961e-18 0.98214 1.0197 1.0577 1.0961 2.9815 1.9756 0.98181
Expectations variables:
EP
_______
0.98214
Define approximation space
interp = recsinterpinit(50,model.sss*0.7,model.sss*1.5);
Find a first guess through the perfect foresight solution
interp = recsFirstGuess(interp,model);
Solve for rational expectations
[interp,Xcat] = recsSolveREE(interp,model);
Successive approximation
Major Minor Lipschitz Residual
0 0 7.61E-02 (Input point)
1 1 0.7086 4.93E-02
2 1 0.5706 3.31E-02
3 1 0.5590 1.55E-02
4 1 0.6546 5.38E-03
5 1 0.6941 1.65E-03
6 1 0.7079 4.81E-04
7 1 0.7122 1.38E-04
8 1 0.7151 3.94E-05
9 1 0.7159 1.12E-05
10 1 0.7163 3.18E-06
11 1 0.7161 9.03E-07
12 1 0.7157 2.57E-07
13 1 1.0000 0.00E+00
Solution found - Residual lower than absolute tolerance
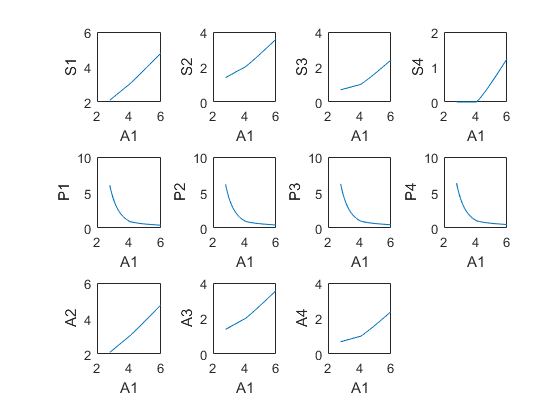
Plot the decision rules
recsDecisionRules(model,interp,[],[],[],struct('simulmethod','solve')); for i=1:model.dim{2} subplot(3,4,i) xlabel(model.symbols.states{1}); ylabel(model.symbols.controls{i}); end
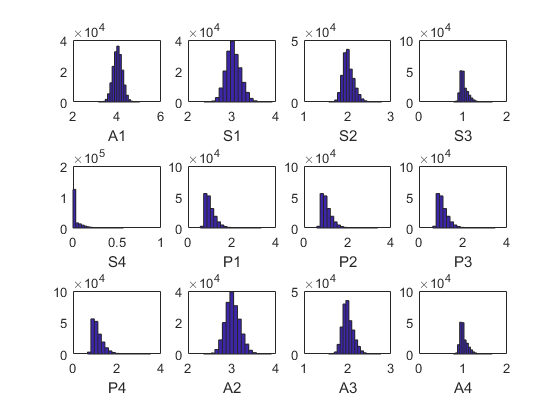
Simulate the model
[ssim,~,~,stat] = recsSimul(model,interp,model.sss(ones(1000,1),:),200,[],... struct('accuracy',1)); subplot(3,4,1) xlabel(model.symbols.states{1}); for i=1:model.dim{2} subplot(3,4,i+1) xlabel(model.symbols.controls{i}); end
Statistics from simulated variables (excluding the first 20 observations):
Moments
Mean StdDev Skewness Kurtosis Min Max pLB pUB
________ ________ ________ ________ _______ _______ ______ ___
A1 4.0339 0.20819 0.045874 3.0194 3.1503 5.0401 NaN NaN
S1 3.0303 0.1669 0.25675 3.1639 2.3639 3.9152 0 0
S2 2.0193 0.12679 0.60361 3.5534 1.5689 2.7836 0 0
S3 1.0207 0.089673 1.2152 4.7192 0.78099 1.6694 0 0
S4 0.034219 0.058308 2.1537 8.0546 0 0.57222 27.647 0
P1 1.0112 0.23947 1.4769 6.0874 0.55524 3.3258 0 0
P2 1.0491 0.24245 1.4769 6.0874 0.58746 3.3925 0 0
P3 1.0875 0.24546 1.4769 6.0874 0.62008 3.46 0 0
P4 1.1263 0.24852 1.4769 6.0874 0.65311 3.5283 0 0
A2 3.0153 0.16607 0.25675 3.1639 2.3522 3.8958 0 0
A3 2.0093 0.12616 0.60361 3.5534 1.5612 2.7697 0 0
A4 1.0156 0.089228 1.2152 4.7192 0.77712 1.6612 0 0
Correlation
A1 S1 S2 S3 S4 P1 P2 P3 P4 A2 A3 A4
________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________
A1 1 0.99865 0.9908 0.95879 0.81734 -0.93754 -0.93754 -0.93754 -0.93754 0.99865 0.9908 0.95879
S1 0.99865 1 0.99649 0.97225 0.84617 -0.91938 -0.91938 -0.91938 -0.91938 1 0.99649 0.97225
S2 0.9908 0.99649 1 0.98842 0.88781 -0.88482 -0.88482 -0.88482 -0.88482 0.99649 1 0.98842
S3 0.95879 0.97225 0.98842 1 0.94735 -0.80621 -0.80621 -0.80621 -0.80621 0.97225 0.98842 1
S4 0.81734 0.84617 0.88781 0.94735 1 -0.57807 -0.57807 -0.57807 -0.57807 0.84617 0.88781 0.94735
P1 -0.93754 -0.91938 -0.88482 -0.80621 -0.57807 1 1 1 1 -0.91938 -0.88482 -0.80621
P2 -0.93754 -0.91938 -0.88482 -0.80621 -0.57807 1 1 1 1 -0.91938 -0.88482 -0.80621
P3 -0.93754 -0.91938 -0.88482 -0.80621 -0.57807 1 1 1 1 -0.91938 -0.88482 -0.80621
P4 -0.93754 -0.91938 -0.88482 -0.80621 -0.57807 1 1 1 1 -0.91938 -0.88482 -0.80621
A2 0.99865 1 0.99649 0.97225 0.84617 -0.91938 -0.91938 -0.91938 -0.91938 1 0.99649 0.97225
A3 0.9908 0.99649 1 0.98842 0.88781 -0.88482 -0.88482 -0.88482 -0.88482 0.99649 1 0.98842
A4 0.95879 0.97225 0.98842 1 0.94735 -0.80621 -0.80621 -0.80621 -0.80621 0.97225 0.98842 1
Autocorrelation
T1 T2 T3 T4 T5
_______ ________ _________ __________ __________
A1 0.21648 0.047568 0.0089635 -0.006843 -0.008623
S1 0.22687 0.050773 0.0094296 -0.0070417 -0.0089489
S2 0.24164 0.055368 0.010032 -0.0073559 -0.0094548
S3 0.2611 0.061608 0.010651 -0.0078625 -0.010267
S4 0.26473 0.064139 0.0099399 -0.0083125 -0.011228
P1 0.13189 0.022645 0.0049882 -0.0058688 -0.0070509
P2 0.13189 0.022645 0.0049882 -0.0058688 -0.0070509
P3 0.13189 0.022645 0.0049882 -0.0058688 -0.0070509
P4 0.13189 0.022645 0.0049882 -0.0058688 -0.0070509
A2 0.22687 0.050773 0.0094296 -0.0070417 -0.0089489
A3 0.24164 0.055368 0.010032 -0.0073559 -0.0094548
A4 0.2611 0.061608 0.010651 -0.0078625 -0.010267
Accuracy of the solution
Equilibrium equation error (in log10 units)
Max Mean
-8.0300 -8.6895
-8.3915 -9.3227
-8.5612 -9.2494
-2.1736 -3.1645
-4.6787 -5.3781
-4.7071 -5.4060
-4.7345 -5.4329
-3.3738 -4.4109
-14.6536 -15.4064
-14.8754 -15.6120
-15.1764 -15.8576