Simulate the model
Running a simulation
Once the rational expectations equilibrium has been found, it is possible to simulate the model using the function recsSimul with the following call:
[ssim,xsim] = recsSimul(model,interp,s0,nper);
where model and interp have been defined previously as the model object and the interpolation structure. s0 is the initial state and nper is the number of simulation periods.
s0 is not necessarily a unique vector of the state variables. It is possible to provide a matrix of initial states on the basis of which simulations can be run for nper periods. Even starting from a unique state, using this feature will speed up the simulations.
Shocks
The shocks used in the simulation can be provided as the fifth input to the function:
[ssim,xsim] = recsSimul(model,interp,s0,nper,shocks);
However, by default, recsSimul uses the function funrand defined in the model object (see Define the model object) to draw random shocks. If this function is not provided random draws are made from the shock discretization, using the associated probabilities.
To reproduce previously run results, it is necessarily to reset the random number generator using the MATLAB function rng.
Asymptotic statistics
If in the options the field stat is set to 1, or if four arguments are required as the output of recsSimul, then some statistics over the asymptotic distribution are calculated. The first 20 observations are discarded (the number of burn-in observations can be adjusted in the options). The statistics calculated are the mean, standard deviation, skewness, kurtosis, minimum, maximum, percentage of time spent at the lower and upper bounds, correlation matrix, and the five first-order autocorrelation coefficients. In addition, recsSimul draws the histograms of the variables distribution.
These statistics are available as a structure in the fourth output of recsSimul:
[ssim,xsim,esim,stat] = recsSimul(model,interp,s0,nper);
Choice of simulation techniques
There are two main approaches to simulate the model once an approximated rational expectations equilibrium has been found.
Using approximated decision rule
The first, and most common, method consists of simulating the model by applying the approximated decision rules recursively.
Starting from a known 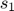 , for
, for 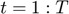
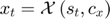
Draw a shock realization 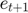 from its distribution and update the state variable:
from its distribution and update the state variable:
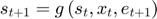
This is the default simulation method. It is chosen in the options structure by setting the field simulmethod to interpolation.
Solve equilibrium equations using approximated expectations
The second method uses the function being approximated (decisions rules, conditional expectations, or expectations function as shown in Solution methods) to approximate next-period expectations and solve the equilibrium equations to find the current decisions (in a time-iteration approach). For example, if approximated expectations (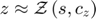 ) are used to replace conditional expectations in the equilibrium equation, the algorithm runs as follows:
) are used to replace conditional expectations in the equilibrium equation, the algorithm runs as follows:
Starting from a known 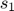 , for
, for 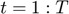 , find
, find 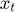 by solving the following MCP equation using as first guess
by solving the following MCP equation using as first guess 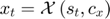
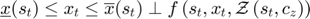
Draw a shock realization 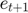 from its distribution and update the state variable:
from its distribution and update the state variable:
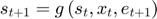
This simulation method is chosen in the options structure by setting the field simulmethod to solve.
The two approaches differ in their speed and in precision. Simulating a model through the recursive application of approximated decision rules is very fast because it does not require solving nonlinear equations. The second approach is slower because each period requires that a system of complementarity equations be solved. However, its level of precision is much higher, because the approximation is used only for the expectations of next-period conditions. The precision gain is even more important when decision rules have kinks, which makes them difficult to approximate. Wright and Williams (1984), who first proposed the parameterized expectations algorithm, suggest using the second method to simulate the storage model.
When does this distinction matter?
Most of the time, the default approach of recursively applying the approximated decision rules should be used. Simulating the model by solving the equations should be considered in the following two cases:
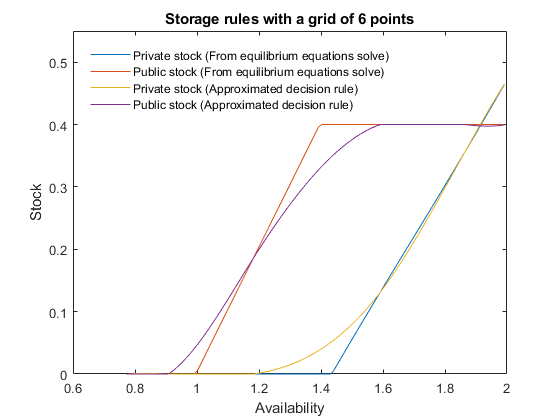
- If the model has been solved with low precision, using the approximated decision rules can lead to large errors, while simulating the model by solving the equilibrium equations using only the approximation in expectations will yield a more precise solution. This applies to the following example inspired from STO2: a price-floor policy backed by public storage. If the problem is approximated by a spline with a small grid of 6 points, it is not possible to expect a good approximation of the highly nonlinear storage rules. However, if the approximation is used only in expectations, it yields a very precise solution:
- If you are interested in the percentage of time spent in various regimes, solving the equilibrium equations is the only way to achieve a precise estimate. Even when solved with high precision, a simulation using the approximated decision rules provides limited precision regarding the percentage of time spent in each regime. Indeed, approximations using spline or Chebyshev polynomials fluctuate around the exact value between collocation nodes. So between two nodes at which the model should be at a bound, the approximated decision rule can yield a result very close to the bound without actually satisfying it. Below are the moments obtained from simulating the model in STO2 with both methods and with decision rules approximated on 30 nodes. The moments are quite similar, but the approximated decision rules widely underestimate the time spent at the bounds:
Long-run statistics from equilibrium equations solve
Statistics from simulated variables (excluding the first 20 observations):
Moments
Mean StdDev Skewness Kurtosis Min Max pLB pUB
__________ _________ ________ ________ _______ _______ ______ ____
A 1.2354 0.11978 -0.24639 2.3466 0.84566 1.5736 NaN NaN
S 0.00067907 0.0049791 9.6845 115.15 0 0.11333 96.467 0
H 1.0026 0.0048614 -0.79925 6.7045 0.96668 1.016 0 0
P 1.0149 0.052212 3.5276 65.956 0.74627 2.3121 0 0
Sg 0.23738 0.11396 -0.33273 2.0936 0 0.4 2.327 8.04
Correlation
A S H P Sg
________ ________ ________ ________ ________
A 1 0.27432 -0.83925 -0.49432 0.99472
S 0.27432 1 -0.4932 -0.49417 0.19462
H -0.83925 -0.4932 1 0.66962 -0.79911
P -0.49432 -0.49417 0.66962 1 -0.41307
Sg 0.99472 0.19462 -0.79911 -0.41307 1
Autocorrelation
T1 T2 T3 T4 T5
_______ _______ _______ ________ ________
A 0.86094 0.74627 0.64798 0.56185 0.48685
S 0.21177 0.13844 0.12202 0.11063 0.10321
H 0.67064 0.49358 0.3821 0.30733 0.25496
P 0.27252 0.15933 0.1057 0.077667 0.057918
Sg 0.8704 0.75827 0.66079 0.57406 0.49735
Long-run statistics if simulated with approximated decision rules
Statistics from simulated variables (excluding the first 20 observations):
Moments
Mean StdDev Skewness Kurtosis Min Max pLB pUB
__________ _________ ________ ________ _______ _______ ______ _____
A 1.2351 0.11989 -0.24965 2.3483 0.84579 1.5726 NaN NaN
S 0.00081005 0.004967 9.378 111.6 0 0.11245 48.809 0
H 1.0026 0.0049023 -0.73036 6.6906 0.96688 1.0163 0 0
P 1.0144 0.051055 4.2926 74.372 0.7466 2.3105 0 0
Sg 0.23685 0.11395 -0.34311 2.0993 0 0.4 1.6 4.554
Correlation
A S H P Sg
________ ________ ________ ________ ________
A 1 0.31155 -0.84109 -0.49756 0.99474
S 0.31155 1 -0.53531 -0.54196 0.23
H -0.84109 -0.53531 1 0.68384 -0.79965
P -0.49756 -0.54196 0.68384 1 -0.41687
Sg 0.99474 0.23 -0.79965 -0.41687 1
Autocorrelation
T1 T2 T3 T4 T5
_______ ________ ________ ________ ________
A 0.86117 0.74661 0.64837 0.56223 0.48724
S 0.18215 0.083958 0.049018 0.03095 0.020311
H 0.67101 0.49373 0.38144 0.30733 0.25531
P 0.29154 0.16 0.10056 0.069375 0.051621
Sg 0.87074 0.75876 0.66132 0.57462 0.49791