Steady state
Steady state definition
The deterministic steady state is the state reached in the absence of shocks and ignoring future shocks. Following the convention adopted in RECS (see Definition of a stochastic rational expectations problem), the deterministic steady state is the set 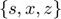 of state, response and expectations variables that solves the following system of equations
of state, response and expectations variables that solves the following system of equations
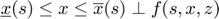
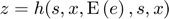
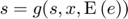
Finding the steady state with RECS
Automatically when initializing model object
When writing a model file (see Writing RECS model files), it is possible, at the end of the Yaml file in the calibration block, to define an initial guess for finding the steady state. When the model object is created by recsmodel, if the definition of the shocks is provided to recsmodel, a Newton-type solver will attempt to find the steady state starting from the initial guess provided in the model file. If a steady state is found, it is displayed in MATLAB command window.
Manually
Otherwise, the steady state can be found manually by feeding the function recsSS with the model and an initial guess for the steady state.
Both approaches rely on a Newton-type solver to find the steady state. See Solvers for systems of nonlinear equations and for mixed complementarity problems for details on solver choice.