First guess

The solution methods used in RECS to find the rational expectations equilibrium of a problem all rely on nonlinear equation solvers that allow convergence only if the starting point is not too far from the solution. Hence, the importance of a good first guess.

RECS can attempt to calculate a first guess that is good in most situations. The method chosen by RECS depends on the model's features. In the absence of complementarity constraints, the first guess is the solution of first-order perturbation around the deterministic steady state. If the model has complementarity constraints, the first guess is the perfect foresight solution of the deterministic problem in which the shocks in the stochastic problem have been substituted by their expectations.

The perfect foresight problem as first guess

It does it by calculating the perfect foresight solution of the deterministic problem in which the shocks in the stochastic problem have been substituted by their expectations:

$\underline{x}(s) \le x \le \overline{x}(s) \perp f(s,x,z),$

$z = h(s,x,\mathrm{E}\left(e\right),s_{+},x_{+}),$

$s = g(s_{-},x_{-},\mathrm{E}\left(e\right)).$

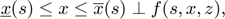
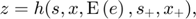
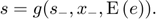
The solver for perfect foresight problems assumes that the problem converges to its deterministic steady state after T periods (by default T=50). The perfect foresight problem is solved for each grid point and the behavior in the first period is used as a first guess for the stochastic problem. This is done by the following call:

[interp,x] = recsFirstGuess(interp,model,s,sss,xss);

This function updates the interpolation structure, interp, with the solution of the perfect foresight problem and outputs the value of the response variables at the first period on the grid, x.

Solving time

As the perfect foresight problem is solved for each point of the grid and for T periods, this step can take some time. In many cases, it should be expected that it may take more time to find a first guess through the perfect foresight solution than to solve the stochastic problem from this first guess.

It is possible to speed up this step by reducing the time horizon from its default values of 50 periods to lower values to the cost of a potentialy less precise first guess. For example, for storage model a time horizon of 5 periods is enough to obtain a good first guess. This is done by changing the options supplied to recsFirstGuess. For example, for a 5-period time horizon:

[interp,x] = recsFirstGuess(interp,model,s,sss,xss,struct('T',5));

Choosing between first-order perturbation and perfect foresight solution

It is possible to force RECS to use one particular method to find a first guess instead of relying on the default option. It is useful if one approach does not provide a good enough first guess or if finding the first guess takes too much time (a usual problem with the perfect foresight solution). If the perturbation approach is adopted with a model including complementarity equations, the bounds are neglected and the first-guess is calculated as if the model was without complementarity equations. For many models with complementarity equations, the first-order perturbation solution provides a first guess that is sufficient to ensure the convergence of the stochastic solver. This choice is done by changing the field fgmethod in the options supplied to recsFirstGuess.

For example, to force the solver to use perturbation:

[interp,x] = recsFirstGuess(interp,model,s,sss,xss,struct('fgmethod','perturbation'));

or to force it to use the perfect foresight approach:

[interp,x] = recsFirstGuess(interp,model,s,sss,xss,struct('fgmethod','perfect-foresight'));

How good is this first guess?

It depends on the model and the approach adopted (and in the case of the perfect foresight approach, it depends also on the solution horizon). For many models, if the state space has been properly defined (i.e., neither too small nor too large), this first guess is good enough to allow the stochastic solver to converge.

The quality of the perfect foresight solution as a first guess depends also on the model nonlinearity. For models with behavior close to linear, the first guess can be extremely good. For example, in the stochastic growth model first guesses from the perfect foresight and the perturbation solutions lead to initial deviations from rational expectations of 1E-5 and 1.3E-4, respectively. So after a few iterations, the solver converges to the solution. However, in the stochastic growth model with irreversible investment, which is much more nonlinear, the residuals when starting the stochastic solver from the first guesses are 1E-2 and 2.8 for perfect foresight and perturbation. This is sufficient to achieve convergence, but it is still far from the true solution.

User-provided first guess

It is not necessary to use the first guess calculated by RECS. A first guess can be provided directly by the user. In this case there is no need to call a function, but only to define a n-by-m matrix x that provides the values of the m response variables for the n points on the grid of state variable. The matrix x should then be supplied to recsSolveREE as would be the one created by recsFirstGuess (see the next step Solve the rational expectations problem for more information).

For example of this, see in demos CS1.